Risk Models

The prediction model together with a (compatible) loss function constitutes a risk model, which can be expressed as .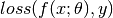

In this package, we use a type SupervisedRiskModel to capture this:

abstract RiskModel

immutable SupervisedRiskModel{PM<:PredictionModel,L<:Loss} <: RiskModel
    predmodel::PM
    loss::L
end

We also provide a function to construct a risk model:

riskmodel(pm, loss)

Construct a risk model, given the predictio model pm and a loss function loss.

Here, pm and loss need to be compatible, which means that the output of the prediction and the first argument of the loss function should have the same number of dimensions.

Actually, the definition of riskmodel explicitly enforces this consistency:

riskmodel{N,M}(pm::PredictionModel{N,M}, loss::Loss{M}) =
    SupervisedRiskModel{typeof(pm), typeof(loss)}(pm,loss)

Note

We may provide other risk model in addition to supervised risk model in future. Currently, the supervised risk models, which evaluate the risk by comparing the predictions and the desired responses, are what we focus on.

Common Methods

When a set of inputs and the corresponding outputs are given, the risk model can be considered as a function of the parameter .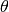

The package provides methods for computing the total risk and the derivative of the total risk w.r.t. the parameter.

value(rmodel, theta, x, y)

Compute the total risk w.r.t. the risk model rmodel, given

• the prediction parameter theta;
• the inputs x; and
• the desired responses y.

Here, x and y can be a single sample or matrices comprised of a set of samples.

Example:

# constructs a risk model, with a linear prediction
# and a squared loss.
#
#   risk := (theta'x - y)^2 / 2
#
rmodel = risk_model(LinearPred(5), SqrLoss())

theta = randn(5)  # parameter
x = randn(5)      # a single input
y = randn()       # a single output

risk(rmodel, theta, x, y)  # evaluate risk on a single sample (x, y)

X = randn(5, 8)   # a matrix of 8 inputs
Y = randn(8)      # corresponding outputs

risk(rmodel, theta, X, Y)  # evaluate the total risk on (X, Y)

value_and_addgrad!(rmodel, beta, g, alpha, theta, x, y)

Compute the total risk on x and y, and its gradient w.r.t. the parameter theta, and add it to g in the following manner: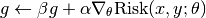

Here, x and y can be a single sample or a set of multiple samples. The function returns both the evaluated value and g as a 2-tuple.

Note

When beta is zero, the computed gradient (or its scaled version) will be written to g without using the original data in g (in this case, g need not be initialized).

value_and_grad(rmodel, theta, x, y)

Compute and return the gradient of the total risk on x and y, w.r.t. the parameter g.

This is just a thin wrapper of value_and_addgrad!.

Note that the addgrad! method is provided for risk model with certain combinations of prediction models and loss functions. Below is a list of combinations that we currently support:

• LinearPred + UnivariateLoss
• AffinePred + UnivariateLoss
• MvLinearPred + MultivariateLoss
• MvAffinePred + MultivariateLoss

If you have a new prediction model that is not defined by the package, you can write your own addgrad! method, based on the description above.