Regularizers¶
Regularization is important, especially when we don’t have a huge amount of training data. Effective regularization can often substantially improve the generalization performance of the estimated model.
In this package, all regularizers are instances of the abstract type Regularizer.
Common Methods¶
Each regularizer type implements the following methods:
-
value(reg, theta)¶ Evaluate the regularization value at
thetaand return the value.
-
value_and_addgrad!(reg, beta, g, alpha, theta) Compute the regularization value, and its gradient w.r.t.
thetaand add it togin the following way: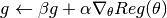
Note
When
betais zero, the computed gradient (or its scaled version) will be written togwithout using the original data ing(in this case,gneed not be initialized).
-
prox!(reg, r, theta, lambda) Evaluate the proximal operator, as follows:
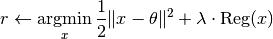
This method is needed when proximal methods are used to solve the problem.
In addition, the package also provides a set of generic wrappers to simplify some use cases.
-
value_and_grad(reg, theta)¶ Compute and return the regularization value and its gradient w.r.t.
theta.This is a wrapper of
value_and_addgrad!.
-
prox(reg, theta[, lambda])¶ Evaluate the proximal operator at
theta. Whenlambdais omitted, it is set to1by default.This is a wrapper of
prox!.
Predefined Regularizers¶
The package provides several commonly used regularizers:
Zero Regularizer¶
The zero regularizer always yields the zero value, which is mainly used to supply an regularizer argument to functions to request it (but you do not intend to impose any regularization).
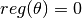
immutable ZeroReg <: Regularizer end
Squared L2 Regularizer¶
This is one of the most widely used regularizer in practice.
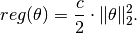
immutable SqrL2Reg{T<:FloatingPoint} <: Regularizer
c::T
end
SqrL2Reg{T<:FloatingPoint}(c::T) = SqrL2Reg{T}(c)
L1 Regularizer¶
This is often used for sparse learning.
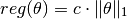
immutable L1Reg{T<:FloatingPoint} <: Regularizer
c::T
end
L1Reg{T<:FloatingPoint}(c::T) = L1Reg{T}(c)
Elastic Regularizer¶
This is also known as L1/L2 regularizer, which is used in the Elastic Net formulation.
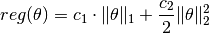
immutable ElasticReg{T<:FloatingPoint} <: Regularizer
c1::T
c2::T
end
ElasticReg{T<:FloatingPoint}(c1::T, c2::T) = ElasticReg{T}(c1, c2)