Risk Models¶
The prediction model together with a (compatible) loss function constitutes a risk model, which can be expressed as 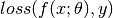 .
.
In this package, we use a type SupervisedRiskModel to capture this:
abstract RiskModel
immutable SupervisedRiskModel{PM<:PredictionModel,L<:Loss} <: RiskModel
predmodel::PM
loss::L
end
We also provide a function to construct a risk model:
-
riskmodel(pm, loss)¶ Construct a risk model, given the predictio model
pmand a loss functionloss.Here,
pmandlossneed to be compatible, which means that the output of the prediction and the first argument of the loss function should have the same number of dimensions.Actually, the definition of
riskmodelexplicitly enforces this consistency:riskmodel{N,M}(pm::PredictionModel{N,M}, loss::Loss{M}) = SupervisedRiskModel{typeof(pm), typeof(loss)}(pm,loss)
Note
We may provide other risk model in addition to supervised risk model in future. Currently, the supervised risk models, which evaluate the risk by comparing the predictions and the desired responses, are what we focus on.
Common Methods¶
When a set of inputs and the corresponding outputs are given, the risk model can be considered as a function of the parameter 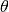 .
.
The package provides methods for computing the total risk and the derivative of the total risk w.r.t. the parameter.
-
value(rmodel, theta, x, y)¶ Compute the total risk w.r.t. the risk model rmodel, given
- the prediction parameter
theta; - the inputs
x; and - the desired responses
y.
Here,
xandycan be a single sample or matrices comprised of a set of samples.Example:
# constructs a risk model, with a linear prediction # and a squared loss. # # risk := (theta'x - y)^2 / 2 # rmodel = riskmodel(LinearPred(5), SqrLoss()) theta = randn(5) # parameter x = randn(5) # a single input y = randn() # a single output value(rmodel, theta, x, y) # evaluate risk on a single sample (x, y) X = randn(5, 8) # a matrix of 8 inputs Y = randn(8) # corresponding outputs value(rmodel, theta, X, Y) # evaluate the total risk on (X, Y)
- the prediction parameter
-
value_and_addgrad!(rmodel, beta, g, alpha, theta, x, y) Compute the total risk on
xandy, and its gradient w.r.t. the parametertheta, and add it togin the following manner:
Here,
xandycan be a single sample or a set of multiple samples. The function returns both the evaluated value andgas a 2-tuple.Note
When
betais zero, the computed gradient (or its scaled version) will be written togwithout using the original data ing(in this case,gneed not be initialized).
-
value_and_grad(rmodel, theta, x, y)¶ Compute and return the gradient of the total risk on
xandy, w.r.t. the parameterg.This is just a thin wrapper of
value_and_addgrad!.
Note that the addgrad! method is provided for risk model with certain combinations of prediction models and loss functions. Below is a list of combinations that we currently support:
LinearPred+UnivariateLossAffinePred+UnivariateLossMvLinearPred+MultivariateLossMvAffinePred+MultivariateLoss
If you have a new prediction model that is not defined by the package, you can write your own addgrad! method, based on the description above.